Canyons Of Mars

Canyons Of Mars

"Slow and steady wins the race" - Not sure about that, but at least we can go for finishing the race...

Following Right Wall

Similarly as in previous years, this brought plenty of mathematics. One was to calculate amount rover needs to steer in order to avoid the wall. Math problem is really as following:

• if we know how much rover traverses each 'tick' (main control loop of "Canyons of Mars" is running at 10Hz),
• if we know what is angle of rover towards the wall

we would like to calculate what is the distance of a point from rover we want it to steer around.

Oh as pictures tell thousands words:

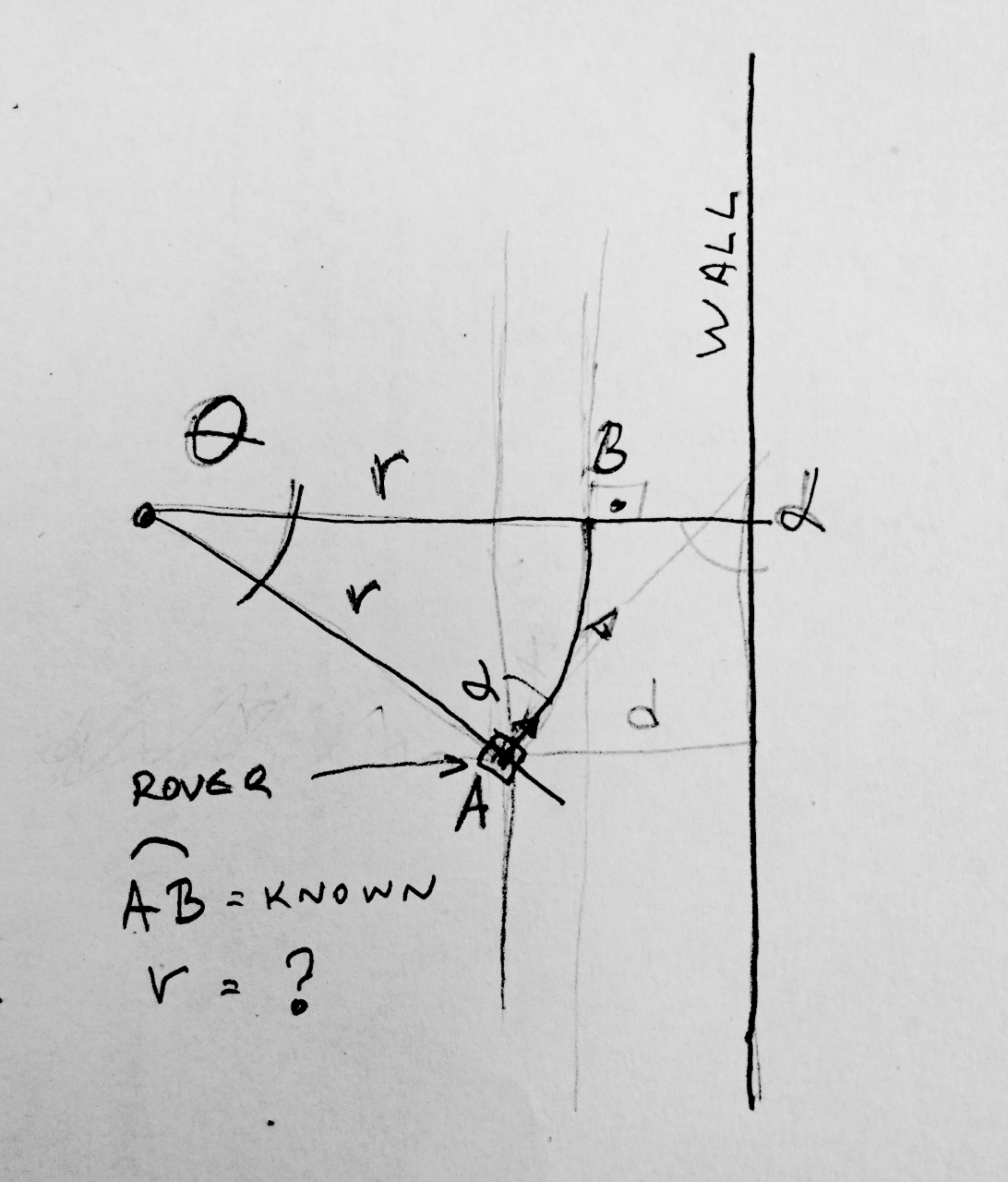
Here we know what arc size is (AB), what distance to wall is (d), angle to the wall (𝝰), we don't know what Θ is but really need to calculate r.

It was interesting seeing how our A level students tackle the problem (coming up with alternate solution and in half the time than me) and how our GCC students do the same.

Anyway - one way to solve it is given on this picture:

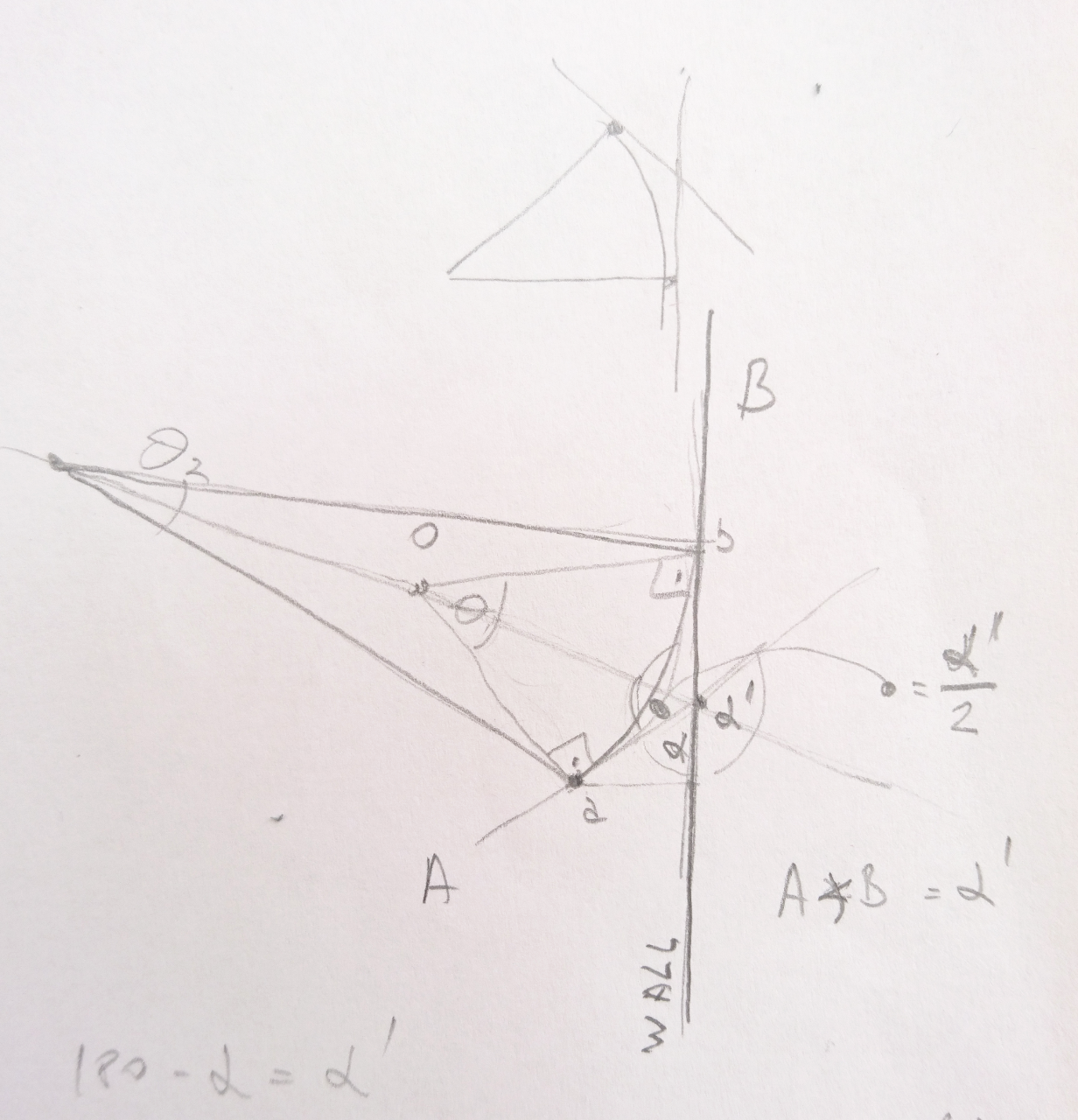
Arc length is r * Θ and using Euclidean geometry we can prove from above picture that Θ is really same as 𝝰. From there it is easy:

length of arch = r * Θ = r * 𝝰 => r = length of arc / 𝝰

And length of arch is really speed our rover is travelling.

Now by the combing distance of point we want rover to steer and angle we want rover to deflect from the wall (if it is too close or get closer if it is too far) we can get really smooth auto correction as what you can see in the video...