The Somewhere Over the Rainbow challenge is new this year and one of the most interesting. We started by breaking down what the rover needs to do for it in simple tasks/steps (no matter how complex each step is):
- turn round the arena at 90º steps (starting with initial 45º turn) - but we need 135º and 180º turns, too
- scan the colour of a ball that that rover is facing
- going towards a corner
- follow left or right wall of the arena to an adjacent corner

Turning around
In Somewhere Over the Rainbow there are several precise angles that the rover should turn:
- 45º at the beginning of the scanning phase
- 90º for scanning each new corner or to visit the next corner
- 135º when facing a corner and needs to go to the adjacent corner on the left or the right
- 180º when visiting the opposite corner
The first (45º) angle is always to one side while the other 90º and 135º are in both directions. For 180º is really doesn't matter which direction it is executed at. We've tried to implement it using internal gyro and PID algorithm. 'P' component says how quickly it should turn, 'D' component dampens it down if it start moving way too fast while 'I' component is giving us a 'nudge' when we are close to the target and speed (PWM percentage) is not enough to really drive motors. When 'D' component is relatively big, 'I' is not collected (reset to zero), but the moment 'D' falls below certain threshold we add errors for 'I' component and it allow us to continue moving when the power could be low
Scanning for Ball Colours
Scanning for ball colours step is 'simple': turn 45º, fetch the colour of the ball we face (and add the first letter of the colour to a string), turn 90º, scan, add to string and repeat. Doing it four times should give us 4 different colours and from the order we can deduct the following steps.
Now, the 'simple' task was originally done by counting RGB pixels and sorting them as red, green, yellow and blue, but that method itself turned to be quite simplistic and not reliable enough. The next blog will explain more about how we used Open CV...
Finding Nemo
Finding a corner is another small autonomous challenge we've done. To do so our V formation of distance sensors works like a charm:
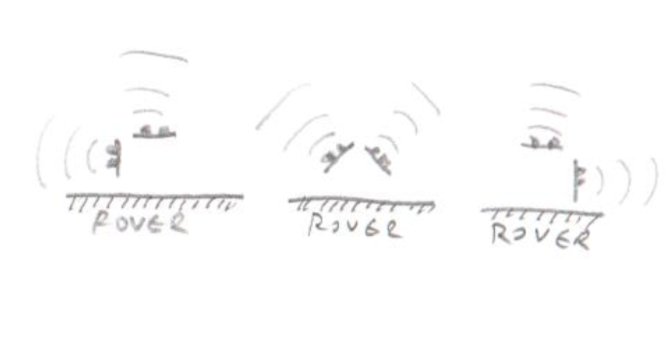 On the picture above we use the middle configuration for this process. The left and right sensor should return a similar distance. If not rover will drive at an angle which would balance distances. Our rover can continue to 'look' forward while driving to the left or right (strafe at some degree). Amount of 'strafe' (angle at which all wheels are going to be) is directly proportionate to proportion of distances of left and right sensor. When left squared distance plus right squared distance is squared target distance (let's say 120 or 150mm) then we've got quite close to the corner. A PID algorithm is responsible for our rover to not slam into the corner nor stopping way too soon. That algorithm will dictate the speed of the rover.
On the picture above we use the middle configuration for this process. The left and right sensor should return a similar distance. If not rover will drive at an angle which would balance distances. Our rover can continue to 'look' forward while driving to the left or right (strafe at some degree). Amount of 'strafe' (angle at which all wheels are going to be) is directly proportionate to proportion of distances of left and right sensor. When left squared distance plus right squared distance is squared target distance (let's say 120 or 150mm) then we've got quite close to the corner. A PID algorithm is responsible for our rover to not slam into the corner nor stopping way too soon. That algorithm will dictate the speed of the rover.
Following Walls
The last piece of the puzzle is following left or right wall. If the next ball is in corner that is left or right to the current corner, the rover just needs to turn 135º and follow the wall. In configuration above it will be one on the left or right. One sensor will be used to judge the distance from the wall and one distance from the corner (opposite wall). The forward sensor will be used with a PID algorithm as above to calculate the speed of the rover. The side sensors will tell us what the rover is supposed to be doing:
- if delta distances (current distance minus previous distance) are close to zero (some small number) rover will continue with driving forward gently strafing to adjust to asked distance from the wall (120 or 150mm).
- if delta distances are increasing - that would mean that rover is going away from the wall and corrective action is needed. That corrective action is calculated as following:
- front sensors deltas will determine rover's current speed and with that speed we can calculate distance rover will travel for one pass of the loop (~ 0.1s as that much it takes for vl53l0x to calculate distance)
- rover will rotate around a point that is a the side of it so circle's arc is of length of calculated travel. That would mean rover will adjust direction so it is parallel to the wall
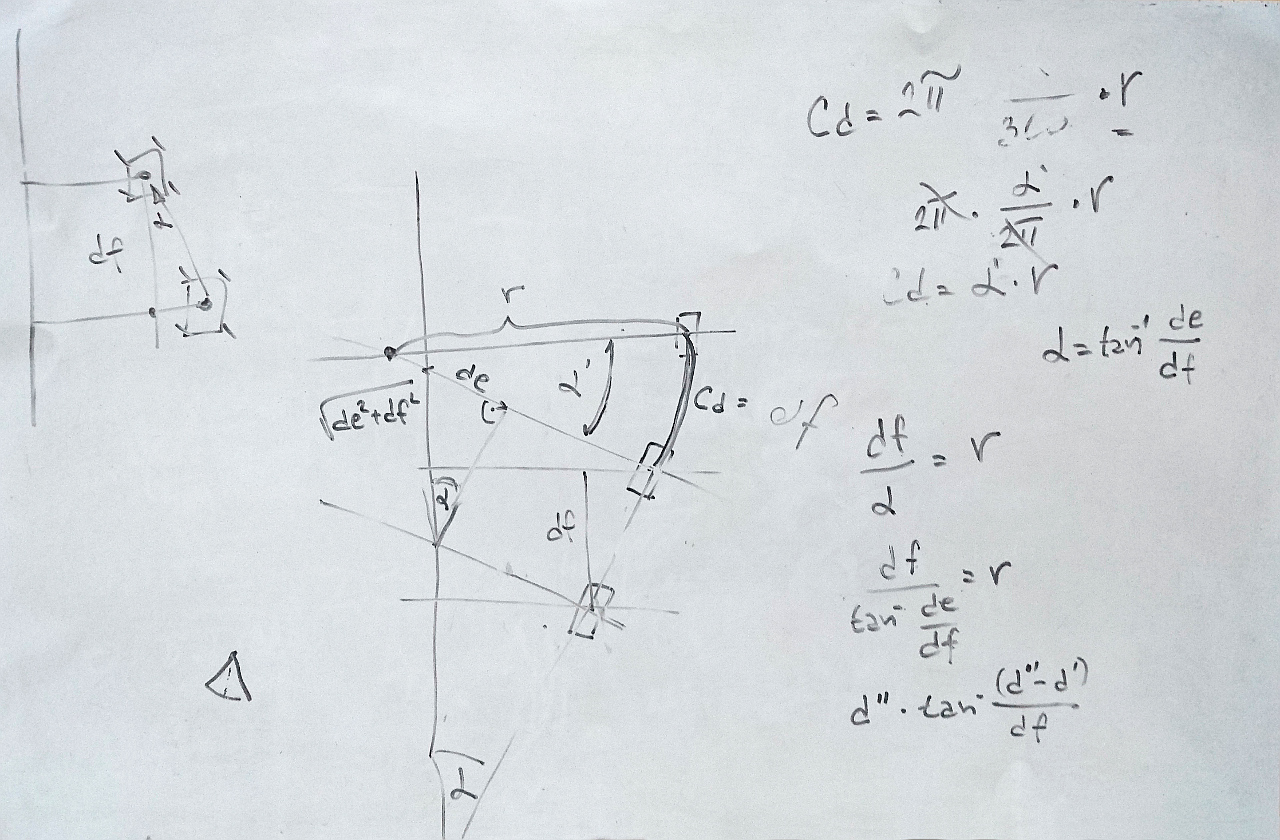
- if delta distances are decreasing - that would mean rover is going towards the wall and similar action as above is needed but around the point at opposite side
With that we can assume by the time the rover arrives to the corner, it will be adequately parallel to the wall no matter which angle it started from. Since the gyro is not absolutely correct (they have a bad tendency to drift) this step is were we expect to correct accumulated errors.
Putting It Together
With the above steps now we can do the challenge.
First we'll turn 45º to face first ball. Then scan, turn 90º and repeat three times to collect all corner colours. If any corner colour is inconclusive we'll put 'X' in the list.
If there are 'X' characters in the list we can turn again to those corners and re-do the scanning until we can determine four distinctive colours. The idea is that if we get two of the same colours out of four - we can just invalidate both and re-scan those corners.
Using OpenCV we can even find the 'moment' (centre) of the ball and adjust required angle to move to the next corner.
When the colour of the balls are determined we need to rotate to the red (shifting our string of colour's first letter accordingly). As a result we'll have a string that always starts with 'R'. Analysis gave us 6 distinct combinations as following:
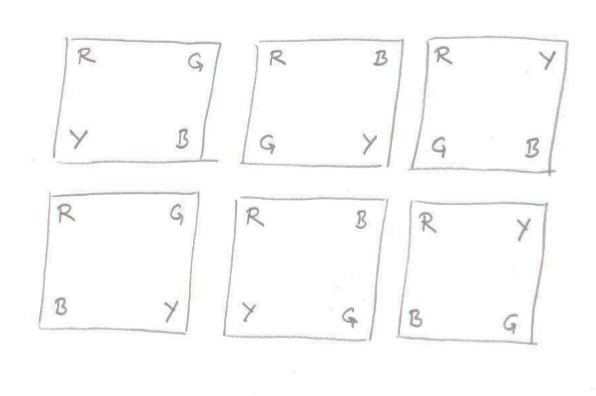 The strings are: RGYB, RBGY, RYGB, RGBY, RBYG or RYBG only! And those 6 combinations can be translated into series of 'find corner'; turn -135º, -90º, 90º or 135º; follow left or right wall! Just as described below. Here are those steps:
The strings are: RGYB, RBGY, RYGB, RGBY, RBYG or RYBG only! And those 6 combinations can be translated into series of 'find corner'; turn -135º, -90º, 90º or 135º; follow left or right wall! Just as described below. Here are those steps:
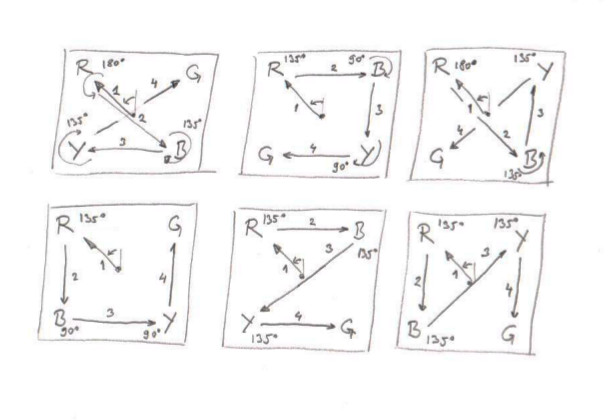 Simple, right?
Simple, right?

 On the picture above we use the middle configuration for this process. The left and right sensor should return a similar distance. If not rover will drive at an angle which would balance distances. Our rover can continue to 'look' forward while driving to the left or right (strafe at some degree). Amount of 'strafe' (angle at which all wheels are going to be) is directly proportionate to proportion of distances of left and right sensor. When left squared distance plus right squared distance is squared target distance (let's say 120 or 150mm) then we've got quite close to the corner. A PID algorithm is responsible for our rover to not slam into the corner nor stopping way too soon. That algorithm will dictate the speed of the rover.
On the picture above we use the middle configuration for this process. The left and right sensor should return a similar distance. If not rover will drive at an angle which would balance distances. Our rover can continue to 'look' forward while driving to the left or right (strafe at some degree). Amount of 'strafe' (angle at which all wheels are going to be) is directly proportionate to proportion of distances of left and right sensor. When left squared distance plus right squared distance is squared target distance (let's say 120 or 150mm) then we've got quite close to the corner. A PID algorithm is responsible for our rover to not slam into the corner nor stopping way too soon. That algorithm will dictate the speed of the rover.
 The strings are: RGYB, RBGY, RYGB, RGBY, RBYG or RYBG only! And those 6 combinations can be translated into series of 'find corner'; turn -135º, -90º, 90º or 135º; follow left or right wall! Just as described below. Here are those steps:
The strings are: RGYB, RBGY, RYGB, RGBY, RBYG or RYBG only! And those 6 combinations can be translated into series of 'find corner'; turn -135º, -90º, 90º or 135º; follow left or right wall! Just as described below. Here are those steps:
 Simple, right?
Simple, right?